Integrales en Bachillerato: paso a paso y sin líos

Las integrales son otro de los grandes temas de Bachillerato y de la EBAU. Al principio parecen complicadas, pero en realidad son el “proceso inverso” a las derivadas.

👉 Idea clave: derivar es calcular la pendiente; integrar es calcular el área bajo la curva.

Las integrales se usan en física, economía, ingeniería… y, por supuesto, en tus exámenes.

1. ¿Qué es una integral y para qué sirve?

Una integral sirve para “sumar infinitas cosas muy pequeñas”. En matemáticas, esto se traduce en:

• Integral indefinida: da una familia de funciones (antiderivada).

• Integral definida: calcula un área exacta entre la curva y el eje X.

👉 Ejemplo real: calcular el área de un terreno con forma curva o la distancia recorrida a partir de la velocidad.

2. Reglas básicas de integración

1. Potencia

Ejemplo:

2. Suma y resta

Ejemplo:

3. Constante

Ejemplo:

3. Interpretación geométrica

La integral definida entre a y b representa el área bajo la curva:

👉 Ejemplo:

Esto equivale al área de un triángulo de base 2 y altura 2.

4. Ejemplos resueltos fáciles

Ejemplo A

Aplica la regla de la potencia:

Ejemplo B

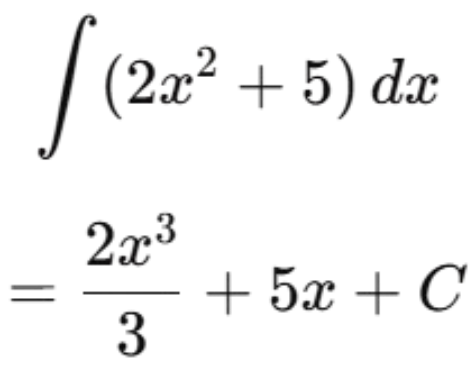
Ejemplo C (definida)

5. Errores típicos en integrales

❌ Olvidar el “+ C” en integrales indefinidas.

❌ Confundir integral con derivada.

❌ No tener en cuenta signos negativos en áreas bajo el eje X.

🚀 Conclusión

Las integrales no son tan misteriosas: con 3 reglas básicas y la idea del área bajo la curva puedes resolver muchos ejercicios de Bachillerato.

👉 ¿Quieres practicar integrales con ejercicios adaptados a tu nivel?

¡Escríbeme aquí!